How viscosity affects centrifugal pumps
The Hydraulic Institute published a standard to account for the effects of viscosity of centrifugal pump performance. Effects of Liquid Viscosity on Rotodynamic Centrifugal and Vertical Pump Performance—available at www.estore.pumps.org—was revised in 2010. Before this publication, viscosity corrections were done using viscosity correction charts.
The new method is much easier to use because it calculates the viscosity corrections automatically by using the formulas provided. The need to "eyeball" from charts has been removed, so the new method is more accurate. The standard also provides a nice background description of the method as well as its limitations and the pump types and pump design characteristics for which the procedure is applicable. The following came as a result of a discussion between several of our readers.
What Are Newtonian Fluids?
Can we assume that crude oil or refined products behave as Newtonian fluids? A key statement is "The viscosity is a function only of the condition of the fluid, particularly its temperature." Water, oil, gasoline, alcohol and even glycerin are examples of Newtonian fluids.
Examples of non-Newtonian fluids are slurries, suspensions, gels and colloids. Perhaps one would feel comfortable with this assumption for crude oil and refined products. But does heavy crude at some point (low temperature) stop behaving as a Newtonian fluid?
Most of the fluids are Newtonian with the basic definition being that viscosity is constant with the shear rate. What is shear rate? It is the relative stress imposed on the fluid by the moving fluid. Consider, for example, a 10–inch, outside diameter (OD) closed impeller, with 0.010-inch radial clearance between the wear rings, which are at a 5-inch diameter. If it rotates at 3,600 rpm, then the metal peripheral velocity is 78 feet per second. The fluid in direct contact with the ring is spinning at the same velocity, according to a no-slip condition. The stationary ring is 0.010 inch away from the motion, so the gradient of velocity is:
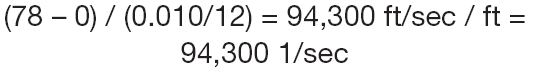
That is the shear rate.
For an open impeller, the distance is between the spinning impeller's open vane and the casing wall. Now the peripheral velocity changes along the radial position of the vane (it is at a little less than 5 inches as compared to the OD of, say, 10 inches). An average value can be estimated (the calculation is similar to the one above), and the shear rate will be similar.
Shear-Sensitive, Non-Newtonian Fluids
Shear-sensitive fluids do not like such shearing action. Glue, for example, gets sticky. Glue, however, is not pumped by centrifugal pumps but more typically by gear pumps. Shear rate, however, still works there as well: in a clearance between the spinning gear and the wall, and such clearance is also typically in the range of 0.005 inch.
Such a shear rate, however, is usually not an issue, as the amount of product in the clearance is small and the overall "dilution" by the sticky, damaged fluid is negligible. In certain cases, though, it does matter. For example, if the fluid pumped by a gear pump is an emulsion deposited on photography film, then even minor imperfections may cause specks and blemishes, and the film ends up defective.
Pumping food—such as cherries, applies, etc.—in the canned food industry raises similar concerns. The pump requirement is gentle pumping with low shear. Progressing cavity pumps work best for these cases.
In a centrifugal pump with clearance between the impeller wall and casing of 0.5 inch, the shear rate is:
![]()

Figure 1. Different types of fluids
Newtonian & Non-Newtonian Fluids and Viscosity
With Newtonian fluids, viscosity does not depend on the shear rate. If pumped oil has a 300-cSt viscosity, for example, it stays so at 3,600 rpm or 1,800 rpm. The shear rate changes, but the viscosity is still 300 cSt.
However for some fluids (non-Newtonian), viscosity does change—either up or down, as shown in Figure 1. These fluids are dilatent or thixotropic. This has an effect on the power required and also may cause fluid degradation, in addition to having an effect (and usually does) on power. Power is force times speed. Force is stress times area. Stress is viscosity times shear rate.
For dilatent fluids shear stress goes up always, as both viscosity and shear rate increase, but for thixotropic fluids it can go either way. Shear rate may not increase as fast as the decrease in viscosity, and the product (stress) can increase, decrease or stay about the same. It all depends on the fluid being pumped. Usually, however, shear stress decreases. That means that power to the pump also decreases with the shear rate. In other words, fluid is first viscous, but once it begins moving, it becomes less viscous, which means less power is required to pump it.
Neglecting the driver rating (motor selected too small) is common. It gets sized for the viscosity of the fluid in motion, but then a motor keeps tripping upon start-up because more power is needed to get things going. Ketchup is one example, and this is why you must shake the bottle like crazy at a restaurant to get it flowing. However once it flows, it does so quickly.
As always—a parting quiz. Why is a "typical" rule-off-thumb that centrifugal pumps do not operate well above the magic number of 500 centistokes viscosity? A correct answer gets you a free admission ticket to the next Pump School session:
www.pumpingmachinery.com/pump_school/pump_school.htm
Pumps & Systems, August 2011
Click here to see a Readers Respond to this article.


