Pumps & Systems, July 2013
Mechanical resonance can be a problem for vertical pumps. Seemingly similar pump designs may operate differently depending on the geometric specifics and the proportions of their rotors. In vertical pumps, long shafting segments are guided by bumper bushings—typically made of bronze, or sometimes, a nonmetallic material.
If the length and diameter of a shaft, or any sections of it between the bushings, fall to a certain ratio, a resonance condition can be encountered. The rotor will “sing” like a guitar string—and unfortunately not a happy song.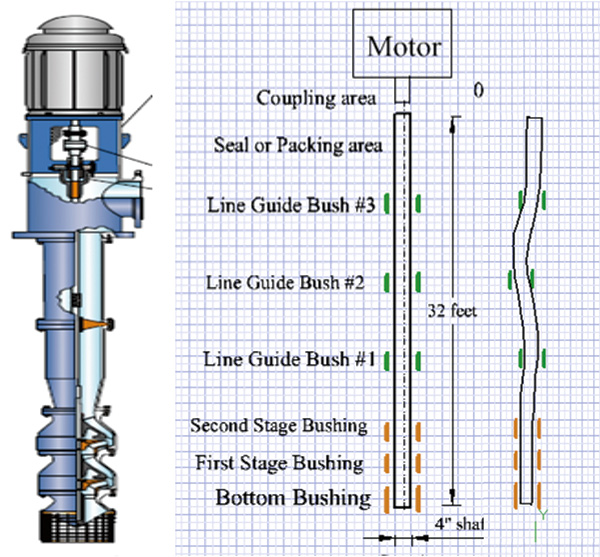
Figure 1. Natural frequency (resonance) can destroy the rotor of a vertical turbine pump
Determining Resonance
To calculate, predict and avoid resonance conditions, pump designers use sophisticated computer programs. The software programs take the following factors into account (among other factors):
- The shaft segments’ lengths
- The shaft’s diameters
- Shaft clearances
- The nature of the pumped liquid (its damping and stiffness characteristics)
However, a lesson can be learned from a simplified formula analysis, which is still used as an estimate. Variations of the formula can assume a shaft segment with ends in different configurations (see Table 1).
Consider a formula for a beam with a uniformly distributed mass. A beam with uniformly distributed mass has infinite natural frequencies. Natural frequencies are arranged in ascending order. The lowest natural frequency is called the fundamental frequency or the fundamental natural frequency.
The natural frequency ωn is determined by:
ωn2 = βn4 x EI / (m/L) [Equation 1]
Where:
E = Young’s modulus of elasticity
I = Moment of inertia of cross section
L = Length of beam (span)
m = Total distributed mass (=W/g)
β1, β2 and β3 for different boundary conditions are shown in Table 1.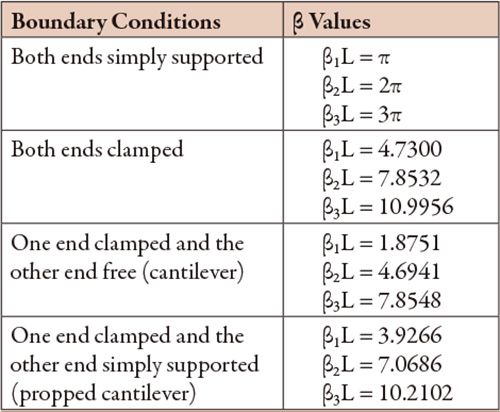
Table 1. β values for boundary conditions
Examples
Using Equation 1, consider a natural frequency case (with both ends of the shaft segments assumed as simply supported) for three shaft diameters (1.44 inches, 1.8 inches and 2.4 inches), for the same 6-foot (72-inch) shaft segment. If this shaft operates at 1,800 rpm (30 hertz), a problematic shaft diameter could be encountered between 1.8 inches and 2.4 inches, causing shaft rotor resonance (see Table 2).
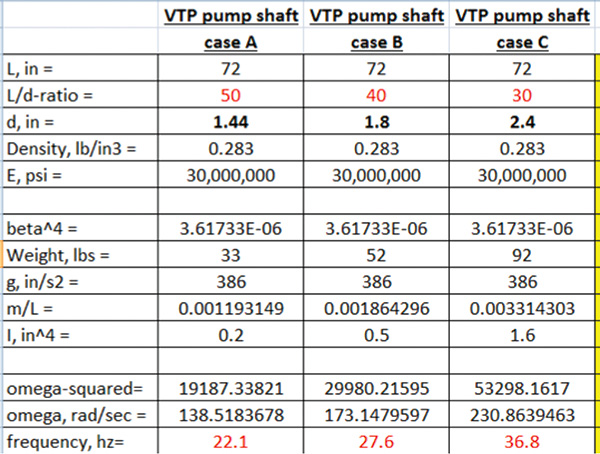
Table 2. Natural frequencies for three shaft diameters
Note: The data is calculated using Equation 1.Table 3. Calculated frequencies for a bar, a human and bacteria
Using Equation 1, natural frequencies of other structures can be estimated, no matter how large or small. In Table 3, a 6-foot steel bar’s natural frequency is calculated at 183 hertz.
A man’s natural frequency (assumed averaged density of bones) is 73 hertz, and a bacterial worm’s is 16 megahertz.
Some interesting examples of structural resonance encountered in life are provided at:
The numbers in this column are estimates, but the concept is clear. Given the right natural frequency, the effects on pumps—and other things—can be bad (or good).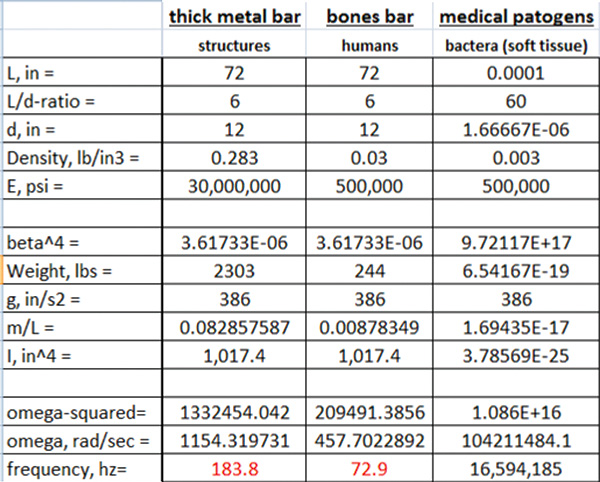
Table 3. Calculated frequencies for a bar, a human and bacteria
Quiz
How would you estimate/calculate a more accurate value for the natural frequencies of biological structures, where shape and densities may not be constant?
The best answers will be published in an upcoming issue of Pumps & Systems. P&S


