Last month we used a hypothetical example to illustrate the onset and effects of water hammer. This month we will investigate its major causes and gain an even better perspective on the variables that contribute to its intensity.
Valve Closure and Opening
One of the primary causes of water hammer is the abrupt closure of a valve. Figure 1 shows a main pipeline with a branch circuit that is fed by a "Tee." At the end of the branch is a valve. The black arrows show the flow direction in the primary and branch lines, and the blue arrow is the length of the branch line. As in last month's example, the valve acts as the primary barrier, but this time the secondary barrier is the "Tee."
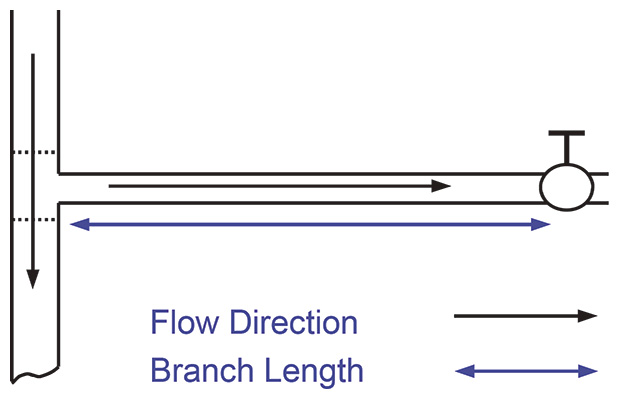
If water is flowing in the branch line and the valve is closed quickly, a shock wave will develop. Its inception follows the same sequence of events in our hypothetical example. One small difference is that some of the intensity of the waves will be lost in the "Tee" as it is open to the main pipeline on either side. Still, a significant portion will be reflected back toward the valve.
A major difference in this example is that we have some control over the valve closure time (in our hypothetical example the valves closed at nearly the speed of light). As you will see, closure time has a significant effect on the inception and intensity of water hammer. Two other variables, flow velocity and pipeline length, are also major factors. The equation P = 0.07 (VL / t) shows the relationship of these three variables and their effect. P is the additional pressure generated by the shock wave, V is the flow velocity in ft/sec, L is the pipe length between the barriers in feet and t is the valve closing time in seconds. 0.07 is a derived constant.
The additional pressure created by the shock wave is directly proportional to flow velocity and pipeline length and inversely proportional to closure time. In other words, higher values of V and/or L will increase pressure while higher values of t will result in a decreased pressure. Table 1 shows the results from this equation when using differing velocities, pipe lengths and closure times. The V values are 5- and 10-ft/sec, L values are 100- and 1000-ft, and t values are 1 and 2 seconds. Two of the variables are constant in each example.

Both columns of the table illustrate the proportional influence of velocity and length—pressure increases as they increase. The lower values in the right hand column illustrate the inverse relationship of time; these pressures are half those in the left hand column because the closure time has doubled. The value of L is often fixed and depends upon the application, but we can exercise substantial control over the other two variables. By doing so, we can eliminate or greatly reduce water hammer's effect.
I mentioned earlier that pipe diameter and the elasticity of its material also influence the pressure generated. Larger diameters and more elastic materials absorb some of the intensity of the shock waves and therefore reduce the pressure generated. Several pipe manufacturers publish curves or tables that show the potential water hammer pressure increase for various pipe diameters and materials.
Suppose that the branch line valve is closed. If it is opened quickly the effect is similar to that of quick closing. When the valve is opened quickly, the branch line sees an immediate drop in pressure, and incoming water from the main line accelerates the previously static column. As friction and other factors restrict its flow, the forward portion of the column can act as the initial barrier and give rise to water hammer. Usually its effect is much smaller than that of valve closure and is often referred to as a "surge." Still, under certain conditions, this surge can be damaging.
Last month, I mentioned that water hammer’s effects can be more significant in low pressure systems. The additional pressure generated by a shock wave is proportional to the length of the pipe and velocity of the water flowing in it and is completely independent of its operating pressure. Therefore, the shock wave created in a 1,000-ft pipe flowing at 5-fps will be the same whether the operating pressure is 50-psi or 200-psi. The difference is the ratio of shock pressure to design pressure can be significantly higher in the low pressure system, therefore the potential for damage will also be greater.
Pump Starts and Stops
In many large pumping systems, it is normal procedure to start a pump against a closed discharge valve. Once the pump is running at full speed, the valve is opened slowly. Flow is initiated and then increases to its maximum as the valve continues to open. This procedure is reversed when a pump is stopped. Starting and stopping against a valve that is opened or closed slowly will inhibit the initiation of water hammer.
Depending upon the installation, the discharge valve may be operated manually or by some automatic mechanism. One of the shortcomings of manually operated valves occurs during a power outage. When a pump motor loses power, the reduction in pump speed and flow from its discharge occur rapidly. The resulting change of kinetic energy to that of pressure can produce water hammer waves in the discharge line. As the water column reverses direction, the impeller will also begin to accelerate backward. When it reaches its maximum reverse speed, backward flow is reduced and an additional pressure surge is created.
In most pressure boost applications, a “spring loaded” check valve is installed at or near the pump discharge and remains closed when the pump is idle. When the pump is started, flow does not begin until the pressure it generates exceeds the pressure on the downstream side of the closed valve. If the downstream pressure is not allowed to decrease below a certain minimum, flow increases slowly and water hammer inception is avoided or reduced significantly.
When the pump stops, an unexpected event occurs—a quick closing valve actually inhibits, rather than initiates, water hammer! In this particular instance, the spring provides quick closure of the valve, which prevents the water column from changing direction due to the higher downstream pressure. Even though flow changes abruptly, pressure remains relatively constant throughout the downstream column. If a standard check valve was installed, the water column would accelerate backward, slam the check closed and initiate a shock wave.
Today, VFD control is used in many applications to eliminate the inception of water hammer during pump starts and stops. This technique, known as soft start and stop, is accomplished by ramping the motor speed up or down over a period of seconds. This allows the flow velocity to increase or decrease much more slowly than it would during across the line starts and stops.
Water Column Separation and Closure
So far, our discussion of water hammer has dealt with single phase systems. In these systems, water remains in a single state (liquid in our examples) regardless of the changes in the hydraulic conditions. The shock waves generated by single phase systems are due to an abrupt change in flow and the resulting transformation of kinetic energy.
The water hammer generated by water column separation and closure is a two phase process. In a two phase system, water changes state and can exist both as a liquid and a vapor within the same confined volume. This phase change can take place whenever the pressure in a pipeline is reduced to that of the vapor pressure of the water. When a pressure drop occurs, the water column can become separated, in one or more locations, by a pocket of water vapor. When the pressure rises above the vapor pressure, the column rejoins or closes and can create a high pressure wave. Water column separation, by itself, can cause problems in very large diameter or thin wall pipes (which can collapse), but water hammer during closure is the more common problem.
Water column separation can occur when a pump is stopped and the water column reverses direction or in condensate lines where high temperatures can mitigate the need for a large pressure drop. Although both forms can be extremely damaging, condensate lines tend to be far more dangerous. The shock waves generated by column closure can travel in opposite directions, and if they hit secondary barriers they can be redirected back toward one another. It would not be unusual for these reflected waves to increase in intensity when they collide. This is certainly the case with water and voltage waves and may account for the often greater damage resulting from closure-initiated water hammer.


